A preliminary study comparing planning target volume-based optimization and robust optimization
Introduction
Proton therapy provides an additional option on treatment modalities to advance cancer care program nowadays. With the scheme of proton therapy alone or combined with other treatment modalities, clinicians have the capacity to expand their practice to address cases that are too complex or too toxic for traditional treatment scheme. Despite the advantage of steep distal dose falloff offered by Bragg peak, proton beam is sensitive to various uncertainties and anatomical changes. Therefore, it is important to ascertain the robustness of treatment plans.
Several studies have evaluated the planning outcome for various treatment sites by using different optimization methods (1-4). The data showed RO could provide better robust plans among different setup and range uncertainty scenarios. As being the first proton center in the country and lacking proton treatment experience in clinical application, we would like to examine the onsite plan quality based on different optimizations and evaluate the consistence with the published results.
In photon treatment, PTV includes internal margin, patient movements, setup and beam inaccuracies to ensure CTV can receive adequate dose. By applying the same concept, expanding CTV via safety margins into PTV which is considering all the impact of stopping power ratio (SPR) conversion, tissue inhomogeneities, organ motion, setup, treatment delivery, etc. By using this PTV, we created one proton plan which is so called herein PTV-based optimization plan. Different from PTV-based optimization, RO optimizes the minimum and maximum doses at each voxel with different range and setup uncertainties to keep the plan robustness (5). The result showed in this study is the comparison data of RO and PTV-based optimization to demonstrate the robustness of IMPT plans.
Methods
In this preliminary study, we selected four cases includes two head-and-neck and two lung cases for robustness plan evaluation. All treatment plans were done on Eclipse treatment planning system version 13.7 (Varian Medical Systems, Palo Alto, CA) and based on line-scanning technique of SHI proton therapy system (Sumitomo Heavy Industries, Ltd). Optimization algorithm was Nonlinear Universal Proton Optimizer (ver 13.0.29). Calculation model was using Proton Convolution Superposition (ver. 13.0.29) with calculation grids of 2.5 mm and spot spacing of 5 mm. For the plans of conventional PTV-based optimization, a planning target volume herein so called PTV was created and used for plan optimization. All the proton uncertainties including range and setup uncertainties were accounted by expanding CTV via safety margins into PTV. For RO plans, CTV and critical organs were optimized by adapting range uncertainty value of 3.5% plus an additional setup uncertainty which are 2 mm for head-and-neck region and 5mm for lung region respectively. The reason our facility chose 3.5% to count for range uncertainty related to stopping power ratio (SPR) estimation is because the value has been well studied (6-8) and considered rather conservative to cover most treatment sites. The planning of lung cases is performing on average free-breath image set and target contour was delineated in MIP (maximum intensity projection) image set of 4DCT imaging. The target motion amplitude is 2.5 mm for lung cases herein.
Results
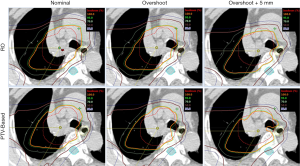
For better illustration of sensitivity to range and setup uncertainties, we compared the dose distributions in transverse plane. Figure 1 is the comparison result of one lung case. Left panels are dose distributions in nominal position; the middle panels are corresponding data with +3.5% over-range, and the right panels are for +3.5% over-range plus 5mm shift in all directions. The underdose regions appeared in the scenarios of overshoot and displacement by using PTV-based optimization, whereas the target remained better dose coverage in the RO plan. This result demonstrates the insensitivity of the RO plan to proton uncertainties compared with the PTV-based optimized plan.
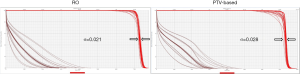
Figure 2 is the DVH for the same lung cancer case. The tables show all range and setup uncertainties for the CTV and spinal cord in the RO plan and the PTV-based plan. The solid lines are the DVHs for the nominal dose distribution which considers no uncertainties appeared. The dashed lines are the DVHs which are concerning different combination scenarios of range and setup uncertainties. By simply comparing the bandwidth in DVH at 50% of the targets compared to PTV-based optimization, we were able to quickly evaluate the plan robustness in defiance of uncertainties. In the figure, it is noticeable that the DVH bands in CTV are narrower for the RO than PTV-based plan. The CTV bandwidth were 0.76 Gy (RBE) in RO, and 3.78 Gy (RBE) in PTV-based optimization. Moreover, the falloff slope of the DVH bands in CTV was steeper, and the maximum dose of spinal cord was lower in the RO plan than PTV-based plan.
Besides from bandwidth comparison, we also used the following equation to calculate a sigma value (σ) so to quantify the distribution of DVH bandwidths in targets for each plan for robustness evaluation. If sigma value is smaller, it indicates the plans has less sensitivity to range and setup uncertainties.
σ=(
The outcome of sigma-value evaluation showed the RO plan was less sensitivity to the uncertainties by reducing sigma-value of 0.008 on average, and dose sparing on critical organs was not compromised.
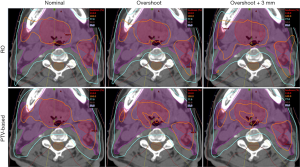
Figure 3 and Figure 4 show the transverse dose distribution and DVH for one head-and-neck case. The dose distribution in the RO plan was insensitive to range and setup uncertainties compared to PTV-based plan. The DVH bands of target was narrower for the RO than PTV-based plan. The sigma value was also smaller which indicates the plan has less response to proton uncertainties. Both the head-and-neck and lung cases showed similar results.

In the dose comparison results for the same lung and head-and-neck cases above, we observed RO led to a slight better target-dose coverage than PTV-based optimization by increasing D95% of CTV about 1.5 Gy (RBE) on average [1.1–1.9 Gy (RBE)], and provide more homogeneous dose distributions by improving HI (D5%/D95%) about 0.03 to 0.04. However, we did not see the significant dose changes on critical organs and the dose difference were mostly within 3 Gy (RBE) between RO and PTV-based plans.
For the other lung and head-and-neck cases both presented similar outcome. The sigma values of CTV were 0.007 [RO], and 0.014 [PTV-based] for the second lung case. For head-and-neck case, the sigma values were 0.018 [RO], and 0.021 [PTV-based]. No significant dose changes on critical organs were observed.
Conclusions
This is a preliminary study to understand the difference among IMPT optimization methods on Eclipse Treatment Planning system with Sumitomo proton system. The study illustrates the treatment plans of PTV-based and robust optimization. The result revealed robust optimization made proton therapy plans less sensitive to proton uncertainties. Besides, compared to PTV-based optimization, RO provided slight superior target-dose coverage and homogeneity without compromising critical organ sparing. The outcome demonstrated traditional PTV-based planning concept in photon treatment has limitations on proton therapy. The superiority of robust optimization was not simply due to the inclusion of safety margins for critical organs, but mainly to the ability of compensating perturbations in dose distributions caused by uncertainties within the volume of targets and critical organs. For the future work, we will expand the evaluation to other treatment sites and include more cases so to have a comprehensive study.
Acknowledgments
Funding: None.
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/tro.2020.03.01). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Liu W, Zhang X, Li Y, et al. Robust optimization of intensity modulated proton therapy. Med Phys 2012;39:1079-91. [Crossref] [PubMed]
- Liu W, Frank SJ, Li X, et al. PTV-based IMPT optimization incorporating planning risk volumes vs robust optimization. Med Phys 2013;40:021709 [Crossref] [PubMed]
- McGowan SE, Burnet NG, Lomax AJ. Treatment planning optimization in proton therapy. Br J Radiol 2013;86:20120288 [Crossref] [PubMed]
- Liao L, Lim GJ, Li Y, et al. Robust Optimization for Intensity Modulated Proton Therapy Plans with Multi-Isocenter Large Fields. Int J Part Ther 2016;3:305-11. [Crossref] [PubMed]
- Yang Z, Li H, Li Y, et al. Statistical evaluation of worst-case robust optimization intensity-modulated proton therapy plans using an exhaustive sampling approach. Radiat Oncol 2019;14:129. [Crossref] [PubMed]
- Yang M, Zhu XR, Park PC, et al. Comprehensive analysis of proton range uncertainties related to patient stopping-power-ratio estimation using the stoichiometric calibration. Phys Med Biol 2012;57:4095-115. [Crossref] [PubMed]
- Moyers MF, Miller DW, Bush DA, et al. Methodologies and tools for proton beam design for lung tumors. Int J Radiat Oncol Biol Phys 2001;49:1429-38. [Crossref] [PubMed]
- Moyers MF, Sardesai M, Sun S, et al. Ion stopping powers and CT numbers. Med Dosim 2010;35:179-94. [Crossref] [PubMed]
Cite this article as: Chou C, Wu T, Huang H, Lee S, Yeh C. A preliminary study comparing planning target volume-based optimization and robust optimization. Ther Radiol Oncol 2020;4:8.