Introduction to accelerators for boron neutron capture therapy
Introduction
This report is the brief lecture for accelerators usable for the intense neutron source for the boron neutron capture therapy (BNCT). Therefore, the lecture does not include the physics of very high-energy accelerators.
BNCT requires the epi-thermal neutrons of which energy range is between 0.5 eV and 10 KeV. Intensity of the epi-thermal neutron should be larger than 109 n/cm2/s for BNCT (1).
Clinical trials of BNCT were carried out until recently by using the nuclear fission reactor as the intense neutron source. Although the effect of BNCT had been confirmed, it was impossible to make the reactor based BNCT in a hospital because of the intrinsic risk of the nuclear reactor. Moreover, a lot of research reactors terminated the operation in the world. As a result, it was started to develop the accelerator as an alternative neutron source instead of the reactor.
There are the MW-class neutron sources based on the large proton accelerators in the world. Spoliation Neutron Source (SNS) is located in the USA. Proton energy of SNS is 1-GeV and its beam power are 1.4 MW (2). In Japan J-PARC is working now. The beam energy and power of J-PARC are 3 GeV and 0.5 MW, respectively. The beam power will be gradually increased to the design value of 1 MW (3). European Spallation Source (ESS) is under construction. It aims to achieve 5-MW proton beam (4). However, spallation neutron sources are not suitable for BNCT because the energy of produced neutrons is too high to be utilized for BNCT. Namely, it requires a heavy moderator/collimator system which leads to an extremely low production efficiency of useful epithermal/thermal neutrons. In addition, a beam shaping assembly needed for the purpose mentioned above will be impractically large.
Even lower energy proton beam can produce the sufficient neutron beam for BNCT if the adequate material is used for the neutron production target and more intense proton beam is accelerated. There are two target candidates such as Lithium and Beryllium. For Lithium, the reaction of 7Li(p,n)7Be is used for the neutron production. Total cross section of this reaction has a peak around 2.3 MeV of proton kinetic energy (5) as shown in the Figure 1. For Beryllium, the reaction of 9Be(p,n)9B is used. The total neutron yield of the reaction is sufficiently large if the proton energy is larger than 5 MeV and it increases gradually as a function of kinetic energy (6) as shown in the Figure 2. Although higher power beam can make more intense neutrons, it makes higher residual does around the target.
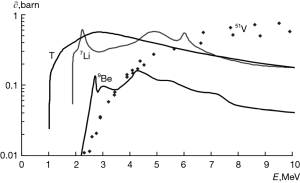
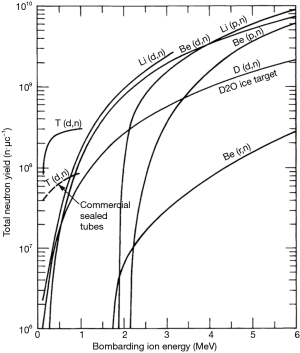
For both target material, we have to consider about the management of the tritium produced by the following reaction:
- for Li target, 7Li(p,n)7Be is main reaction. However natural lithium includes 6Li of 7.6%. It has the reaction 6Li(n,t)4He by the neutron made by the main reaction;
- for Be target, 9Be(p,t)7Be reaction is opened if the proton energy is more than 13.4 MeV.
Deuteron and electron beam
Until here, the beam is assumed proton. However other particles are also usable. Most effective particle for neutron production is deuterium D which consists of weakly coupled a proton and a neutron. When the accelerated D collides the target, the weakly coupled neutron of D is easily decoupled from proton and emitted to forward direction of the beam. However, we have to consider the effect of the beam loss in the accelerator. In particular, it has to be considered the period of the beam commissioning of an accelerator. During the beam commissioning period, it is unavoidable to loss the beam in the accelerator even if the beam intensity is very low. Therefore, it easily expects that the residual dose induced by D beam is much larger than that by proton or electron.
For electron beam, beam tuning is much easier and expected residual dose around the accelerator is low enough. However, the neutron production efficiency is not so high because almost beam energy is spent for the electromagnetic shower production. Thus, the electron beam is not adequate for BNCT. For instance, all of the large neutron facilities described above use the proton beam. Thus, the proton is assumed as the accelerated beam in this report. Furthermore, the energy of proton is assumed also a few 10 MeV in maximum. Then, this lecture describes the just low energy accelerator.
Principle of the particle accelerator
Electro-static accelerators
An ion (or a charged particle) is accelerated by the electric field generated by a static electric potential or a radio frequency (RF) electro-magnetic microwave. In this section, electric-static accelerators are explained.
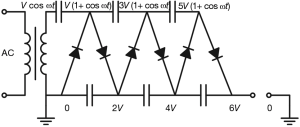
Electro-static accelerator is the simplest device to accelerate the ions. There are two types of the high voltage generator. First one is called Cockcroft-Walton accelerator uses the rectifier invented by Cockcroft and Walton (7). The generator circuit is shown in Figure 3. It can induce approximately 1 MV in maximum. Cockcroft-Walton accelerator succeeded the first nuclear conversion by using the artificially accelerated charged particle beam in the world at 1932 (8). Early proton linear accelerator for high-energy physics laboratory used the Cockcroft-Walton accelerator as the front-end injector. Figure 4 shows the 750-kV Cockcroft-Walton accelerator at KEK in Japan which was used until a start of J-PARC. The size of it is huge as shown in the figure. However almost Cockcroft-Walton accelerators has been replaced with radio frequency quadruple (RFQ) linac which is described in the following section.
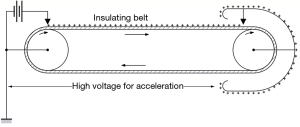
Another electro-static accelerator uses Van de Graaf high voltage generator (9). The generator accumulates the electric charge in the metal sphere which induces the electric potential by using the rotating belt or a chain with insulated pellets which transport the charge as shown in Figure 5. For proton acceleration, positive charge is accumulated and proton source is located inside the sphere positively charged up.
Tandem accelerator is an application of Van de Graaf. It accelerates negative ions at first from outside where is electrically ground level to the inside positively charged up area. Then the orbital electrons of the ion are stripped in order to convert the negative ion to the positive ion. The positive ion is accelerated again to the outside. Therefore, the ion is accelerated twice in the accelerator. The size of the tandem accelerator is relatively compact if the total voltage is less than a few MV. Thus, it is a candidate for the BNCT with the lithium target.
RF accelerator
In this section we describe two types of the linear accelerator (linac) and a cyclotron. First one is a drift tube linac (DTL). Second one is a RFQ linac. Both use the standing wave of the high-power RF electro-magnetic field in the cavity for the acceleration of the charged particles. Cyclotron is not linac because the beam orbit is spiral.
Before the explanation of the linac, it should be discussed at first for the patterns of the standing wave of RF field in the cavity.
RF field in the cavity
The RF electro-magnetic wave put into a cylindrical cavity made of a material forms the standing wave if the RF wave has a specified frequency fixed by the size of the cavity. Copper is common material of the cavity because it has good electrical conductivity. Almost smaller cavities are made of copper. Bigger ones are made of iron or stainless-steel as a construction material of which the inside surface is coated by copper layer.
The standing wave patterns are derived from Maxwell equations in vacuum (10). The equations are
rot E = −∂B/∂t, rot H = ∂D/∂t + J, div D = ρ, div B =0,
[E: electric field, B: magnetic field, D: electric displacement, H: the magnetic intensity, J: conduction current density. Boldface fonts (E, B, etc.) mean a vector.]
where D = ε0E, B = µ0H (ε0: vacuum permittivity, µ0: vacuum permeability).
In the cavity, J=0 and ρ=0. Then we get finally the following three dimensional-wave equations:
∆E − µ0ε0∂2E/∂t2=0, ∆H − µ0ε0∂2H/∂t2 =0.
If both of E and H have the harmonic time dependence exp(-jωt), these are converted to the Helmhorz equations;
∆E + k0E =0, ∆H + k0H =0 (k02 = ω2µ0ε0).
These can be solved with the boundary conditions which are (1) E must be perpendicular to the inner surface of the cavity (2), H must be parallel with the inner surface of the cavity.
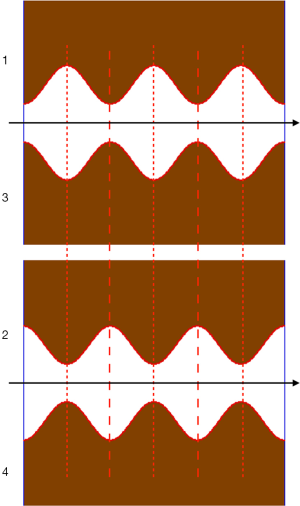
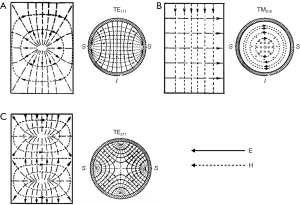
The standing wave mode has two types which are called the transverse electric (TE) mode and the transverse magnetic (TM) mode, respectively. TE mode has no electric field component of z-direction in the cylindrical coordinate r-θ-z. For TM mode, the magnetic field has no z-component. Some examples of the solutions for the cylindrical cavity are shown in the Figure 6. It shows E-H patterns of the modes. The lowest frequency of TM mode is TM010 mode. It has uniform electric and magnetic pattern along z direction and the highest azimuthal symmetry. TM010 mode is most common mode for the accelerator application. For TE mode, TE111 and TE211 modes are used for linac.
Alvarez DTL
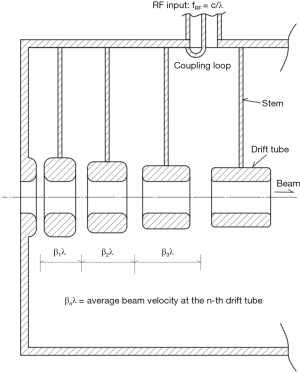
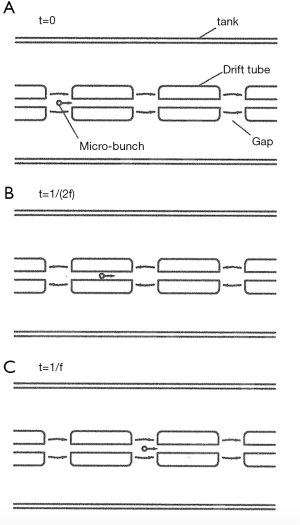
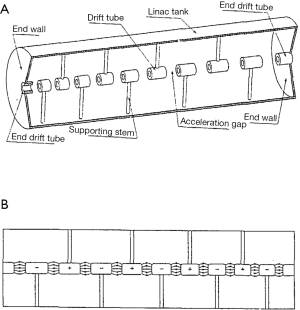
DTL invented by Alvarez (11) is the most common accelerator for proton beam. It uses TM010 mode of a cylindrical cavity. The RF frequency is commonly chosen between 200 and 450 MHz. However, it is impossible to accelerate the particle to the desired direction in the simple cylinder because the field direction inverts periodically. Therefore, Alvarez installed small cylinders called a drift tube (DT) in the center of cavity which has a small bore-hole particle pass through. Each DTs are supported by a stem from the cavity cylinder as shown in Figure 7. DT woks as a kind of shield of the RF electric field. The RF electric field which is concentrated in the gap between the adjacent DTs is changed its direction at every half period of the RF cycle. However, we want to use only the field which accelerates beam. DT prevent the deceleration of the beam in the DT by the opposite oriented electric field as shown in Figure 8 because the bore radius of DT is sufficiently smaller than the wave length of RF field so that the field decreases rapidly in the bore-hole. From the above description, it is obvious that DTL cannot accept the whole continuous beam but can accelerate a part of the beam. In other words, the beam injected into DTL must be bunched.
As beam is accelerated in the gap, it become much faster than before. Thus, the moving distance of the bunch of beams per one RF cycle become longer. In order to synchronize the phase of RF field cycle with the particle position, a space from the center of a gap to that of the next gap must be increased gradually. The increment of the space and the length of DT is calculated by the designed energy gain at each gap. Since DTL uses TM010, the electric fields in all gaps oscillates in phase. As an example, the inside of DTL of J-PARC is shown in the Figure 9. Inner surface of all instrument is covered by the copper layer or made of copper.

As moving particles certainly have the transverse velocity component, some focusing device must be required to keep the beam near the ideal orbit in the cavity. Therefore, DT contains the compact quadrupole magnets (Q-mag), which can focus/defocus the beam, in the DTL. The cross-sectional view of the Q-mag is shown in Figure 10. In the figure it is assumed that the beam axis is perpendicular to the paper and beam moves from top of the paper to the behind. Q-mag has two kind of pole layout. The beam is focused horizontally and defocused vertically in the left side Q-mag by the Lorentz force F = qv × B (v: velocity of the particle). This Q-mag is called the focusing Q-mag. The right side of the figure is the defocus Q-mag. Magnetic field strength of Q-mag is a linear function of the distance from the beam axis. If the focus and the defocus Q-mag are represented by F and Q, respectively, each DT has F or D magnet. F-D pair is required for focus the beam for both of horizontal and vertical direction. Thus F-D-F-D is standard layout. Although F-F-D-D is also possible, the low energy part of the high intensity linac does not use this layout because the stronger focusing force is required against the repulsion force induced by the space charge of the bunched beam.
Although DTL is usually used to accelerate the proton beam up to almost 50 MeV for high-energy accelerator, the beam energy of near 10 MeV is adequate for BNCT with Beryllium target. DTL can accelerate the proton beam of the approximately 100-mA peak current in maximum. The duty factor [repetition rate of beam pulse (Hz) × beam pulse length(s)] of less than 10–20% is reliable for a long-time stable operation.
Inter-digital H-mode DTL
Inter digital H-mode (IH) DTL is another DTL which use TE111 mode. Original TE111 has no electric field along the beam axis. Thus, DTs in IH linac are supported by stems extended from the both side of the cavity alternatively as shown in the Figure 11 (12). It is seemed that the fingers of the right and left hand join alternatively. It is the origin of the name of “inert-digit”. Electric field direction of neighboring gap is opposite.
IH structure is mainly adopted by a heavy ion linac of lower beam intensity because of the following reasons:
- accelerating electric field has transverse field component because the original field is TE111. As the beam deflected by the residual transverse field, the beam is kicked transversely. Thus, beam quality become worse;
- DT in IH linac has no Q-mag because DT is too small. As a result, Q-mags are set at outside of cavity. Thus, it is hard to confine the intense beam around the beam axis.
However, IH DTL is preferred for a heavy ion linac because it has a higher field gradient than that of the Alvarez DTL. Thus, the ring accelerator for carbon therapy uses the IH DTL as an injector.
RFQ linac
RFQ linac was invented by Kapchinskii and Teplyakov at 1969 (13) and it became popular in the world in the 1970’s after the design method was established by Los-Alamos National Laboratory (14). As mentioned in the DTL section, a common RF linac can accelerate only the bunched beam in phase of RF wave. As the beam from an ion source is continuous dc beam, a beam bunching must be required. RFQ can not only accelerate the bunched beam but also bunch the injected dc beam.
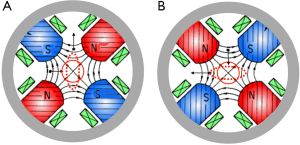
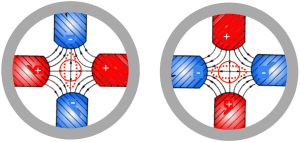
RFQ linac has four electrodes called vane as shown in Figure 12. RF mode of RFQ linac uses is the TE211 mode which is deformed by the vanes. The vane 1 and 3 have the same potential. The vane 2 and 4 have also the same potential. It works as an electric quadrupole for focusing the beam as shown in Figure 13. If the vane has uniform shape along the beam axis, the electric field in RFQ has no component along the beam direction so that the simple RFQ cannot accelerates the beam. In order to make the accelerating electric field, vanes of RFQ is not uniform but modulated as shown in the Figure 14. Vane 1 and 3 have the miller symmetric modulation. Vane 2 and 4 have also the same symmetric shape. However, the modulation period of vane 1 and 3 is suited a half period from that of vane 2 and 4 as shown in Figure 14. In other words, the position of the summit of vane 1 and 3 is adjusted to the position of the valley of the vane 2 and 4. As an electrical force line chooses the shorter path, the line cross from the summits of the vane 1 and 3 to those of vane 2 and 4. As a result, the electric field vector has not only the quadrupole field but also a component along the beam axis which can accelerate or decelerate the beam. Therefore, the electric field in RFQ has both of focus and acceleration functions.
RFQ linac has three sections which have the different functions. These are the matching of radial emittance section, the beam bunching section and acceleration section, respectively. The direct current (DC) beam from the ion source has a time independent characteristic. However, the acceptance ellipse of RFQ for radial direction depends on the time (RF phase). The radial matching section, in which vanes have tapered shape without modulation, gives the matched time dependent structure to the DC beam. In the following bunching section, a part of the dc beam is accelerated and other part of them is decelerate because the vane modulation is started from this section. Finally, the continuous beam is bunched. The velocity of the beam bunch center is not changed in the bunching section. After the bunching, the modulation pattern of vane is gradually shifted from bunching to full acceleration of the beam in order to achieve the design energy of RFQ.
The beam energy of RFQ is from approximately 2.5 to 3 MeV commonly. Thus, RFQ can produce the sufficient neutrons by itself for BNCT with Lithium target. Of course, RFQ is also usable for the injector to DTL. The peak beam current of almost 50 mA and the duty factor of 10–20% in maximum is suitable for the stable operation.
Cyclotron
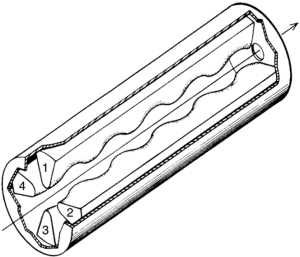
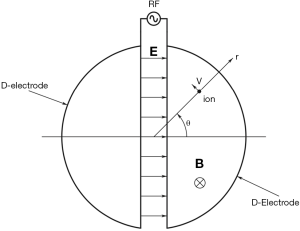
Moving charged particle of which velocity is v has a circular motion under the uniform magnetic field B if v is perpendicular to B. When B is constant, the circulating radius is proportional to the velocity. However, one turn period T (=2πm/eB) does not depend on the velocity of the particle. It is an isochronous condition. Lawrence and Livingston introduced a pair of semi-circles shaped hollow electrodes, which are called “D (or Dee)”, in the magnet in order to accelerate the bunched beam (15) as shown in Figure 15. Because alternative voltage is applied to the Ds, electric field appears in the gap between both the Ds. Frequency of the alternative voltage has to be tuned to the circulating frequency fixed by the magnetic field strength and the ration e/m (e: an electric charge number of ions, m: mass of ion) of the particle (ion). Then, the circulating particle is accelerated twice during one turn. Orbit radius is increased because the velocity increases by the acceleration. Thus, the shape of the orbit becomes a spiral. Finally, the beam is extracted to the outside of the electrode by using a deflector.
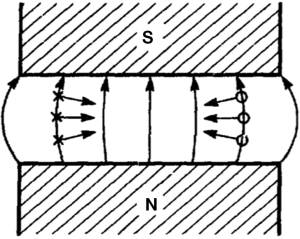
Until here it is assumed that direction of the particle velocity is exactly perpendicular to the magnetic field and the magnetic field is uniform. However, the moving direction of the particle is never perpendicular to the magnetic field so that the real orbit is not kept in the medium plane in the D. Thus, it collides the electrode soon. Therefore, a focusing mechanism is required to keep the circle orbit in the medium plane. In cylindrical coordinate, the magnetic strength B is represented B = B (Br, Bθ, Bz). If B = B (0, 0, Bz), the beam focusing is impossible. However, B = B (Br, 0, Bz) and (∂Br/∂z) <0, the beam has a focusing force for the vertical (z-axis) direction as shown in Figure 16. From rot B =0 because the field is static, ∂Br/∂z = ∂Bz/∂r. Then (∂Bz/∂r) <0 is the condition for the vertical focus of the beam.
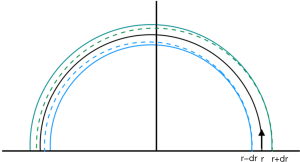
Focus for the radial direction requires another condition. ∂Bz/∂r > −Bz/r. Let prove it intuitively. Bz = Bz(r) is assumed. The r0 denotes the radius of the standard orbit. Suppose that a particle is shifted dr from r0. If Bz = Bz(r0)(1– dr/r0), the orbit radius of the particle shifted dr becomes r = r0 + dr. Figure 17 shows the three semi-circles which correspond to dr =0, >0, <0, respectively.
If Bz > Bz(r0)(1-dr/r0) when dr >0, the orbit radius decreases and its orbit closes to center one. When dr <0, it requires Bz < Bz(r0)(1-dr/r0) to increase the orbit radius. These are the requirement for the horizontal focus of the beam.
Series expansion of Bz(r) is as follows:
Bz(r) = Bz(r0) + (∂Bz/∂r)dr +…= Bz(r0)(1+(∂Bz/∂r)(r0/Bz(r0))dr/r0+…)
Due to the comparison of the second term of Bz = Bz(r0)(1−dr/r0), the condition (∂Bz/∂r)(r/Bz)=−1 is derived. Furthermore if (∂Bz/∂r)(r/Bz) >–1, Bz(r) fills the horizontal focus condition described just before.
If we define n called the field index as n=–(∂Bz/∂r)(r/Bz), horizontal focus condition is n<1. Furthermore the condition of (∂Br/∂z) <0 for the vertical focus is converted to (∂Bz/∂r)(r/Bz) <0 because ∂Br/∂z = ∂Bz/∂r and r/Bz >0. Namely n>0. We can summarize the focus condition as 0<n<1. This means that the magnetic field should decrease along the radius for the beam focus. It is called the weak focus. (Focus system using the Q-mags is called the strong focus.)
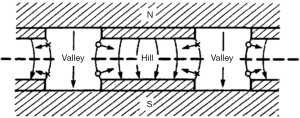
However, the weak focus condition breaks the isochronous condition because B is not constant. Furthermore, the effects of relativistic kinematics must be considered in the higher energy. As a result, the weak focusing conventional cyclotron is not usable for proton which has the energy more than approximately 10 MeV. The azimuthally varying field (AVF) Cyclotron proposed firstly by Thomas is possible to use for the higher energy acceleration of proton (17). The magnetic field of the AVF Cyclotron is varied by changing the gap size of magnet as shown in the Figure 18. Wide and narrow gap region of the magnet are called the valley and the hill, respectively (16). Beam feels the strong focusing force which is similar to the force of the Q-mag at the boundary between the hill and the valley. Furthermore, the magnetic field is increased with the radius of the beam orbit in order to compensate the relativistic effect and keep the isochronous condition. Cyclotron for BNCT is usually AVF type because the proton energy is higher (20–30 MeV). The detail of the theory of AVF cyclotrons is in the reference. The beam current of the common cyclotron is 1–2 mA.
Ion source
Proton is made from Hydrogen gas. Hydrogen molecule H2 is decomposed into protons and electrons so that plasma is formed. Conventional plasma production method uses the hot cathode made of the filament of tungsten (W) or LaB6 as an electron source. When the electric current flows in the cathode, the temperature of the cathode increases due to the electric power loss caused by the electric resistance of the cathode. As a result, thermal electrons emitted from the cathode collide the Hydrogen molecules around the cathode and ionize them.
Another method uses the electron cyclotron resonance (ECR). ECR utilizes the circular cyclotron motion of the electron excited by the RF field under the fixed magnetic field. As mentioned before, the cyclotron motion fills the condition of f = eB/(2πm). For instance, if we apply the RF field of 2.45 GHz, which is the most common frequency of the magnetron for a microwave oven, and the magnetic field of 0.0875 T, electrons circulate resonantly in the plasma chamber. Although it needs free electrons as seeds, gas contains a few free electrons commonly. Under the ECR condition, circulating electrons ionize the hydrogen molecules and make the total number of electrons increase. Thus, plasma production is progressed rapidly.
Plasma is produced in the metal chamber. The electron is easily absorbed at the metal surface. Thus, we have to confine the plasma in the center region of the chamber. Ion source typically uses two types of the magnetic field layout for the electron confinement.
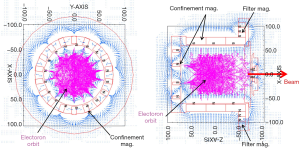
Multi-cusp magnetic field has a multipole magnetic field induced by the even number permanent magnets arranged azimuthally of the cylinder of plasma chamber with the alternative magnetic field layout. Figure 19 shows the schematic view of the cross section of the multi-cusp magnet layout and magnetic field. It also shows the simulation result of electron orbit. By this field electrons cannot arrive the inside surface of the chamber. Hot cathode type ion source commonly uses the multi-cusp type magnetic field to confine the electrons.
Another magnetic field layout for the electron confinement is the magnetic mirror with two solenoids. Electrons have curling motion around the line of magnetic force and is reflected at the both side where the magnetic field is squeezed, which is called the magnetic mirror effect. Thus, the electrons are confined in the middle region between two solenoids. Schematic view of the magnetic mirror is shown in Figure 20. Magnetic mirror with two solenoids is suitable for the ECR ion source because it is possible to choose the magnetic field strength so as to achieve the ECR condition.
Finally, protons are extracted from the plasma chamber pass through the hole by applying the electric high voltage. Although the static extraction voltage from 50 to 100 kV is commonly used, the pulse voltage is occasionally applied for chopping the beam pulse.
Interaction of the charged particle with materials and target structure
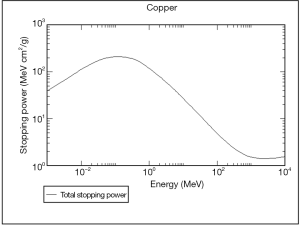
The moving charged particle, which is an ion or an elementary particle such as proton for instance, interacts with the material through the electro-magnetic force. The interaction excites and/or ionizes atoms of material so that the moving particle loses its kinetic energy gradually in the material. The fraction of energy loss per path length dE/dx is described by Bethe-Block formula modified by Sternheimer et al. (18) which includes the quantum mechanical effect. dE/dx of proton in copper (19) is shown in Figure 21. When the charged beam stops in the material, it has a large peak of the energy deposit just before it comes to rest called Bragg peak (20) as shown in the Figure 22. It is derived by the numerical integration of the Bethe-Block equation. The ion beam therapy uses the Bragg peak to destroy the tumor cells.
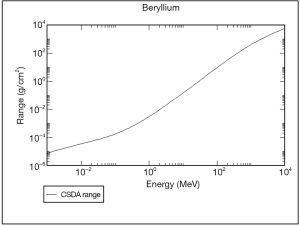
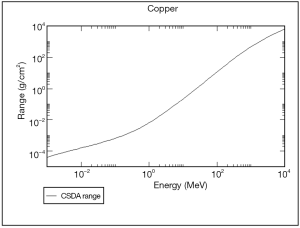
The range is the moving distance of the particle until it is almost at rest. It is also calculated from dE/dx. Figures 23,24 show the results of the range of proton in Be and Cu, respectively. For instance, the range of 8-MeV proton is 0.1 g/cm2 for Be and 0.15 g/cm2 for Cu, respectively. Since the densities of Be and Cu are 1.9 and 8.9 g/cm3, ranges are 53 and 169 µm, respectively.
The protons which stop in the metal change to the hydrogen gas by taking free electrons from the metal. The hydrogen gas breaks the metal by the blistering soon. Thus, manufacturing of the target against the blistering is serious problem of BNCT.
Several groups developed the target which has the multi-layer structure. The first layer is Li or Be for neutron production. It should be thin so that the proton does not stop in the material. The proton has the Bragg peak in the second layer just behind the Li or Be. Material of the second layer is a kind of hydrogen storage metal. It must accumulate the protons injected into the target in order to avoid the blistering by hydrogen gas. Third layer is a cold plate made of copper for instance.
Issues of the target manufacturing are as follows:
- selection of the hydrogen storage metal or alloy;
- how to bond the layers;
- how to cool the target because proton beam power becomes a few 10 kW.
To be honest, the target may be the most difficult equipment of the accelerator based BNCT system at the present time.
Conclusions
A clinical practice of BNCT was being continued by using neutrons from the nuclear fission reactor. However, it is hard to install the reactor in the hospital. Thus, an accelerator is considered recently as a good candidate of the neutron source because the small proton accelerator is adequate for BNCT in a hospital. There are several candidates of the accelerator for BNCT. Although the principle of a few types of proton accelerator has been explained in this report, it is not easy to choose one of them because accelerator specifications depend on the target design of which the manufacturing method is still under development. The comparison for accelerators is summarized in the Table 1. RF linac, Tandem electrostatic accelerator and Cyclotron are usable for the BNCT application. The construction cost and the treatment of residual dose are real issues for accelerators. The characteristics of the neutrons produced by an accelerator is not different from the neutron characteristics of the nuclear reactor because the modulator which is installed behind the target is designed to make the characteristics of the accelerator produced neutrons resemble to the neutron characteristics of the nuclear reactor.
Table 1
| Parameters | Electro-static accelerator | RFQ | RFQ + DTL | Cyclotron |
|---|---|---|---|---|
| Kinetic energy (MeV) | 2.3 | 2.3 | 6–13 | >20 |
| Beam structure | DC | Pulse | Pulse | DC |
| Peak beam current (mA) | ~2 | 30–50 | 30–50 | 1–2 |
| Ave. beam current (mA) | ~2 | 2–5 | 2–5 | 1–2 |
| Target material | Li | Li | Be | Be |
| Pros | (I) Stable; |
(I) Compact; |
(I) Target is stable; |
(I) Target is stable; |
| Cons | (I) Target is unstable; |
(I) Target is unstable; |
(I) Two cavity tuning is not easy; |
(I) Beam energy > ~20 MeV because of lower beam current. (Higher energy proton has a larger neutron yield.) as a result; |
BNCT, boron neutron capture therapy; RFQ, radio frequency quadruple; DTL, drift tube linac; DC, direct current.
Acknowledgments
The author would like to thank Dr. Kumada and Prof. Chen for giving me the opportunity to write the review of the accelerator for BNCT. This is the one and only experience for me.
Funding: None.
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors (Hiroaki Kumada and Yi-Wei Chen) for the series “Boron Neutron Capture Therapy” published in Therapeutic Radiology and Oncology. The article has undergone external peer review.
Conflicts of Interest: The author has completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/tro.2018.10.11). The series “Boron Neutron Capture Therapy” was commissioned by the editorial office without any funding or sponsorship. The author has no other conflicts of interest to declare.
Ethical Statement: The author is accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- IAEA. Current status of neutron capture therapy. Vienna: International Atomic Energy Agency, 2001:7.
- Champion MS, Dean RA, Galambos JD, et al. Progress on the proton power upgrade of the spallation neutron source. Available online: http://accelconf.web.cern.ch/AccelConf/ipac2017/papers/tupva147.pdf
- Hasegawa K, Hayashi N, Oguri H, et al. Performance and Status of the J-PARC Accelerators. Available online: http://accelconf.web.cern.ch/AccelConf/ipac2017/papers/tupva090.pdf
- Garoby R. Progress on the ESS project construction. Available online: http://accelconf.web.cern.ch/AccelConf/ipac2017/papers/moxba1.pdf
- Taskaev SY. Accelerator Based Epithermal Neutron Source. Phys Part Nuclei 2015;46:956. [Crossref]
- Hamm RW. Multi-purpose neutron generators based on the radio frequency quadrupole linear accelerator. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/4142/0000/Multipurpose-neutron-generators-based-on-the-radio-frequency-quadrupole-linear/10.1117/12.410581.full
- Cockcroft JD, Walton ET. Experiments with High Velocity Positive Ions. (I) Further Developments in the Method of Obtaining High Velocity Positive Ions. Available online: http://rspa.royalsocietypublishing.org/content/136/830/619
- Cockcroft JD, Walton ET. Experiments with High Velocity Positive Ions. (II) The Disintegration of Elements by High Velocity Protons. Available online: http://rspa.royalsocietypublishing.org/content/137/831/229
- Van de Graaff RJ, Compton KT, et al. The Electrostatic Production of High Voltage for Nuclear Investigations. Phys Rev 1933;43:149. [Crossref]
- Collins RE. Foundations for Microwave Engineering. New York: McGraw-Hill Book co., 1966.
- Alvarez LW, Bradner H, Frank JV, et al. Berkeley Proton Linear Accelerator. The Review of Sci Ins 1955;26:111. [Crossref]
- Yamada S, Hattori T, Fujino T, et al. IH Linac development at INS. Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/17/065/17065226.pdf
- Kapchinskii IM, Teplyakov VA. A linear ion accelerator with spatially uniform hard focusing. Prib Tekh Eksp 1970;2:19-22.
- Crandall KR, Stokes RH, Wangler TP. RF QUADRUPOLE BEAM DYNAMICS DESIGN STUDIES. Available online: http://accelconf.web.cern.ch/AccelConf/l79/papers/s4-1.pdf
- Lawrence O, Livingston MS. The Production Of High Speed Light Ions Without The Use Of High Voltages. Phys Rev 1932;40:19. [Crossref]
- Craddock MK. High-Intensity Circular Proton Accelerators. In: Hyder AK, Rose MF, Guenther AH. (eds) High-Brightness Accelerators. New York: Plenum Press, 1988.
- Thomas LH. The Paths of Ions in the Cyclotron I. Orbits in the Magnetic Field. Phys Rev 1938;54:580. [Crossref]
- Sternheimer RM, Seltzer SM, Berger MJ. Density effect for the ionization loss of charged particles in various substances. Phys Rev 1987;26:6067. [Crossref]
- Berger MJ, Coursey JS, Zucker MA, et al. Stopping-Power & Range Tables for Electrons, Protons, and Helium Ions. Available online: https://www.nist.gov/pml/stopping-power-range-tables-electrons-protons-and-helium-ions
- Okamura Y. Energy loss and Range of the charged particle in matters. Available online: http://www.nucl.phys.titech.ac.jp/presen/data/thesis/b/ay2008/okamura/Bthesis.pdf
Cite this article as: Naito F. Introduction to accelerators for boron neutron capture therapy. Ther Radiol Oncol 2018;2:54.