Evaluation of dose calculation accuracy of treatment planning systems in the presence of tissue heterogeneities
Introduction
Dose calculation accuracy in treatment planning systems (TPS) varies significantly in the presence of tissue inhomogeneities. This can lead to unacceptably large differences between calculated and delivered doses and hence misleading treatment plans for lung stereotactic body radiotherapy (SBRT) patients. Successful radiotherapy demands dose accuracy of better than 5% (1,2). This is predicated on accurate treatment simulation within a TPS before radiotherapy can begin.
A typical TPS is equipped with multiple dose calculation algorithms. Generally, these algorithms boast either calculation speed or accuracy, but not both. In lung treatment planning, most TPS use a standard dose algorithm with fast calculation times that approximate the effects of lateral electron scattering (3), in the presence of tissue density differences in the thorax region. Although the calculations are quick, these algorithms can lead to substantial dose delivery errors.
Recent developments of accurate and relatively fast Monte Carlo (MC)-based dose calculation algorithms have promising new implications in lung treatment plans. These MC-based algorithms are becoming more accessible but are still not widely available or are fast enough for consistent use in a TPS; however, if treatment conditions under which MC-based algorithms provide a significant advantage over standard algorithms can be well-defined, their clinical implementation could lead to more accurate and reliable treatment plans in lung cancer patients.
A number of recent studies have been done to investigate treatment conditions under which MC-based dose algorithms are ideal. A paper by Chen et al. (3) suggests that the reliability of standard dose algorithms is dependent on tumor size, and that MC-based dose calculations are needed most in the treatment of small lesions. This is because electronic disequilibrium effects are exaggerated in smaller treatment geometries (4). Similarly, other groups including Carrasco et al. (5) have demonstrated that standard dose algorithms perform poorly for smaller field sizes. However most of these studies were restricted to testing dose calculation accuracy of limited number of TPS in a synthetic phantom at a single institution. Thus, any dose differences related to the clinical implementation of various TPS were not studied.
In the present investigation, a common CT study set was mailed to three institutions with explicit instructions for planning dose calculations. Their results were then inter-compared. The institutions were selected to provide a variety of TPS currently used for lung SBRT. The goals of the study are to: (I) validate the accuracy of a commercial MC-based algorithm against measurements; (II) compare performance of the following five dose calculation models: MC; pencil beam (PB); two versions of convolution superposition (CS); and a model based on the solution to linear Boltzmann transport equation (LBTE). A final goal of this study is to identify clinical situations where the accuracy of MC algorithm is most desirable and make recommendations for lung treatment planning.
Methods
Phantom construction
To investigate the impact of tissue heterogeneities on dose distribution, four custom phantoms were built with materials having a range of densities (ρ) relative to water: tissue-equivalent plastic water (Model PW, CIRS Inc., Norfolk, VA, USA) (ρ=1.032), lung-equivalent cork (ρ=0.306), and bone material (ρ=1.895). These materials were chosen based on CT scans which showed HUs (Hounsfield units) comparable to those of structures in the thorax region (Table 1).
Table 1
| Phantom materials | Dimensions (mm): L × W × H | Density (g/cm3) | HU (Ave.) | HU (SD) | Thorax tissues | HU (Ave.) | HU (SD) |
|---|---|---|---|---|---|---|---|
| Cork | 300×300×60 | 0.306 | −728 | 41 | Lung | −775 | 143 |
| Plastic water | 300×300×300 | 1.032 | 58 | 15 | Tissue | 38 | 10 |
| Bone | 300×300×30 | 1.895 | 648 | 38 | Bone | 511 | 185 |
Hounsfield units (HU) for these materials and for the corresponding thorax anatomy are also listed.
We designed the following test phantoms: homogeneous tissue-equivalent; heterogeneous lung; heterogeneous bone; and dual lung-target phantoms (Figure 1). The dual lung-target phantom represents a particularly challenging case for lung SBRT where two adjacent targets separated by lung density tissue need to be treated. Furthermore, this is a good test case to examine dose algorithm accuracy in the lung-tissue interface region. All phantoms in this study consisted of several 300×300 mm2 slabs of varying thickness with total phantom thickness of 200 mm.
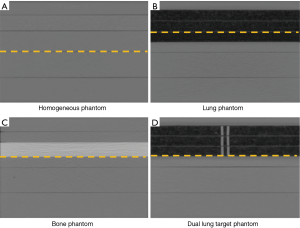
- The homogeneous phantom consisted of plastic water slabs with dose measurement planes at depths of 30, 60, 100 and 150 mm.
- The lung phantom contained 20 mm of plastic water followed by 60 mm of lung equivalent cork material followed by 120 mm of plastic water. This phantom allowed dose measurement planes at depths of 20, 40, 60, 80, 100 and 150 mm.
- The bone phantom consisted of 50 mm of plastic water followed by 30 mm of bone equivalent material followed by 120 mm of plastic water. Dose measurement planes for bone phantom were at depths of 30, 50, 80, 100 and 150 mm.
- The dual-lung target phantom was composed of 20 mm of plastic water followed by 60 mm of lung equivalent material followed by 120 mm of plastic water. Two adjacent tissue equivalent targets were embedded within the cork. The dimensions of each target were 5 mm × 50 mm × 60 mm with 5 mm uniform separation between them. Dose measurement planes for the dual-lung target phantom were at depths of 20, 40, 60, 80, 100 and 150 mm.
Whereas doses were measured and calculated in all available planes, dotted lines shown in Figure 1 represent the measurement planes for which results are reported in this paper.
CT simulation and treatment planning
All phantoms were scanned on a Phillips Brilliance 16-slice CT (Philips Corporation, Ohio, USA) scanner using 2.0 mm slice separation. Several “dummy” films (Kodak EDR2 films, Kodak Corporation, Rochester, New York, USA) were placed at the location of measurement planes within each phantom to mimic treatment geometry (6). For dose calculations, all CT scans were exported to three different TPS:
- BrainLAB iPlan version 4.2: BL PB convolution, and MC dose model;
- Philips ADAC Pinnacle version 9.10: PL Collapsed Cone Convolution/Superposition (CCC) dose model;
- Varian Eclipse version 11.0.31: VR Analytical Anisotropic Algorithm (AAA), Acuros XB dose model.
Using measured beam data, each institution modeled a Novalis 6MV linear accelerator with micro multi-leaf m3-collimators (MLC) in their respective TPS. Results of TPS calculations were validated by comparing depth dose and profile scans in water (homogeneous phantom conditions) for a variety of field sizes with measured data. A common Hounsfield-unit-to-electron-density (HU2ED) curve required for dose calculations was used with all TPS except for Acuros XB. This curve was created by scanning a CT electron density phantom (Gammex Corporation, Inc., Middleton, WI) with 16 inserts of various materials ranging from low-density lung (electron density relative to water, ρe=0.29) to cortical bone (ρe=1.69). For Acuros dose calculations, a standard material table provided by the vendor (Varian Corporation, Inc.) was used for calculations. Treatment plans were created using a single 6MV photon field incident on the phantom in a SAD setup at the depth of 100 mm. Four field sizes covering the range of field-dimensions commonly used in the lung treatment planning were used: 12 mm × 12 mm, 24 mm × 24 mm, 30 mm × 30 mm, and 60 mm × 60 mm. A field size of 100 mm × 100 mm was used for the film calibration purposes. All treatment fields were defined on a Novalis 6MV linear accelerator with micro multi-leaf m3-collimators (MLC). The collimator jaws were set at 100 mm × 100 mm for all treatments. Surface to source distance (SSD) ranged from 895 to 900 mm, depending on the phantom used. First, a MC plan was generated on the iPlan TPS to deliver 2 Gy dose to the isocenter and the monitor units (MUs) recorded. Calculation grid size was 2 mm and the heterogeneity corrections were turned on for all treatment plans. Then dose calculations were performed without changing MUs obtained from the MC plan. These MUs were also used in irradiating each phantom. The films used in the phantom irradiation were the same type as the “dummy” films used in the CT setup (Kodak EDR2 films, Kodak Corporation, Rochester, New York, USA). Films were placed at various depths in the phantom to investigate effects of tissue-heterogeneities on delivered dose. Doses were measured both within and outside the heterogeneous medium as well as the boundaries or tissue/lung/bone interfaces.
TPS and dose calculation algorithms
The treatment planning software (BrainLAB iPlan ver. 4.2) is equipped with a two-dimensional pencil beam convolution (PBC) algorithm (7,8). In PBC model, the incident beam is considered composed of several pencil-like beamlets as they pass through the patient and deposit dose. The PB dose kernel is scaled according to the medium density along the beam direction. A major approximation of the model is that nearest neighbor interaction (side-scatter) between adjacent beamlets is ignored. This results in reduced accuracy of dose calculation in the low-density medium. The TPS has been upgraded to allow MC dose calculations based on an X-ray Voxel MC algorithm (9,10). It was thus decided to investigate accuracy and clinical implications of the MC dose model in iPlan. MC calculations were performed to calculate dose-to-medium using 1% dose variance and a 2-mm grid size. We also investigated the effects of using a finer dose variance of 0.5% (results not reported in this work).
Pinnacle Collapsed cone convolution (CCC) uses a 3D CS model to calculate dose in the patient (11,12). The incident fluence is modeled as a 2D fluence distribution and projected through the patient to calculate a 3D TERMA distribution which is later convolved with a dose kernel at each point to determine final dose. To improve calculation speed, dose at each point is calculated only along the center of each TERMA cone. The algorithm is able to accurately calculate dose distributions in regions of electronic disequilibrium, such as, tissue-air and tissue-bone interface.
Varian Eclipse AAA is a CS dose model that is like the PB, but more sophisticated as it considers density scaling in all three dimensions (13,14). AAA uses a multiple-source model to represent the photon beam and its interaction in a patient is modeled as density scalable poly-energetic kernels. The use of analytical Gaussian functions in convolution speeds up AAA calculations and makes it practical for routine use in a TPS. Acuros XB is based on solving the LBTE for the interaction of X-rays and electrons with matter (15-17). It is assumed that the particles only interact with the medium but not with each other in the process of depositing dose. LBTE can be solved by either statistical methods (MC) or by explicit numerical methods (Acuros XB). Just like MC methods, Acuros XB uses some discretization approximations in grid/angle/energy spacing to speed up the calculation. This can however result in differences in dose calculation accuracy.
EDR film dosimetry
All films were processed using a Kodak M35A X-OMAT film processor (Kodak Corporation, Rochester, New York, USA) in our department. The temperature in the processing room was kept constant (developer at 34.4 °C and processor at 48.9 °C). Films were scanned using a Vidar VXR16 Dosimetry Pro film scanner (Vidar Systems Corporation, Herndon, VA, USA). The scanner communicated with Radiological Imaging Technology version 4.0 (RIT, Colorado Springs, CO, USA) film scanning software on Windows XP computer. Orthogonal profiles and percent depth-dose (PDD) curves were obtained and exported using the RIT software. Films were scanned at a resolution of 89 µm and preprocessed with a median (5×5) filter to remove local film artifacts. All phantom measurements performed with the film were normalized to the central axis measurement in a 98 mm × 98 mm field geometry. Optical density was calibrated from a sensitometric (H&D) curve constructed in the dose range 0–600 cGy. Delivered film doses were confirmed to be in the linear range of the H&D curve. Film measurements were further verified using a small volume (Scanditronix/Wellhofer CC13, 0.13cc) ion chamber in a large volume (500×500×500 mm3) water phantom.
Data analysis
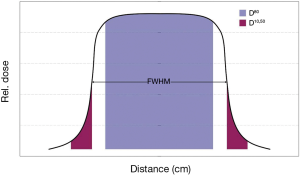
Measured and calculated dose profiles were compared using several dose parameters, namely, area under the central 80% of the profile curve, dose asymmetry (difference between left and right sided areas), FWHM (full-width at half of maximum dose value), beam penumbra (or skin thickness from 90–10% dose level) and dose-spill outside the radiated field from 50–10% dose level (see Figure 2).
To evaluate dose differences between measured and calculated profiles, we define a dose-index (Ddiff) that combines the dose under the central 80% of the curve with FWHM for each profile
where, Ddiff is the dose difference index between the measured and calculated doses; D80 is the area under the dose profile within the central 80% of the field in Gy-mm (or %-mm); F is the full-width at half of maximum dose value, and the subscripts m and c refer to measured and calculated (PB, MC, AAA, Acuros XB, or Pinnacle) doses respectively.
We also define a dose spill index (Dspill) that accounts for differences in dose delivered to regions outside the field (target) as the ratio of the area under the dose curve between 10% and 50% dose levels:
where, D10,50 represents the area under the dose-profile curve between 50% and 10% of the maximum dose.
The above dose indices, Ddiff and Dspill were evaluated and compared as a function of field size, phantom depth, and the heterogeneities (soft-tissue, lung, and bone).
Results
Phantom 1: homogeneous phantom
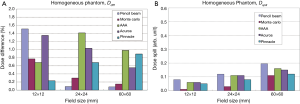
For homogeneous phantom, there is excellent agreement (<2%) between all TPS calculations and measured PDDs/dose profiles for all field sizes and depths (Figure 3). MC calculations show excellent agreement with measured data to within 1%. For all TPS, dose differences between calculation and measurement are generally larger for smaller fields: <1.5% for 12 mm field size compared to <1% for 60 mm field size (Figure 4).
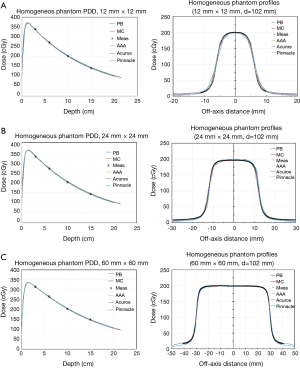
Small but systematic dose differences are seen in regions outside the treatment field (Dspill). Overall, MC is the most accurate predictor of dose in the penumbra region followed by Pinnacle CCC, VR Acuros, VR AAA, and BL-PB. In contrast to the central axis dose, dose spill differences tend to increase with field size (Figure 4).
Phantom 2: heterogeneous lung phantom
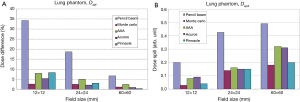
In the lung phantom, which provides a good test case for model comparisons, there is again excellent agreement between MC and measured doses (<3%) for all field sizes and depths (Figure 5). This agreement is seen to improve with increasing field sizes (12 to 60 mm). For example, after going through 40 mm of cork (d=64 mm), MC calculations differ from measured data by 2.6% for 12 mm × 12 mm field and 1.1% for 60 mm × 60 mm (Figure 6). However, at the same depth, PB calculations significantly over-predict the measured dose by as much as 34% for a 12 mm × 12 mm field. Even for larger fields, PB still over-predicts the measured dose albeit by a smaller amount (6.7% for 60 mm × 60 mm field). The calculated and measured dose differences in the treatment field center for other TPS are smaller and range between 7.5% at 12 mm × 12 mm field size and 2% at 60 mm × 60 mm. Within the treatment field, Acuros XB shows the closest agreement with measurements, however the penumbra is broadened. The central axis dose agreement with measured data for other TPS is in the following order: Pinnacle CCC, AAA and PB.
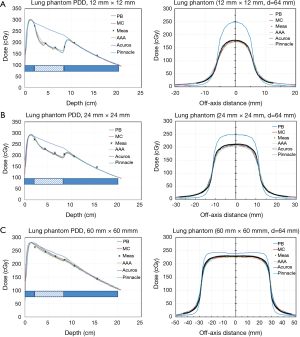
Besides the central axis dose differences, the PDD calculations show interesting behavior in the interface regions, where the best agreement is seen with MC followed by Pinnacle, Acuros, AAA and PB TPS. Both AAA and PB show a lack of sensitivity to changes in dose caused by the interface between tissue and lung. Based on the PDD comparison, both Acuros and Pinnacle can accurately model dose in the interface regions leading to the closest agreement with MC model and measurements. AAA appears to be somewhat insensitive to density differences near interfaces resulting in an over-prediction of dose in moving from soft-tissue to lung and an under-prediction of dose in from lung to soft-tissue. There appears to be an insensitivity or spatial-lag in dose response to tissue-density differences within AAA.
Outside the treatment field, dose spill differences between calculations and measurements increase with field size for all TPS. Again, MC results are in better agreement with the measured data than PB calculations. The agreement with measurements in the penumbra region for other TPS is: MC followed by Pinnacle, Acuros, AAA and PB.
Phantom 3: heterogeneous bone phantom
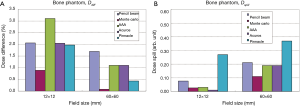
In the bone phantom, there is excellent agreement for central axis dose between MC calculations and measured data for all fields (Figure 7). The agreement improves with increasing field size (from <1% for 12 mm × 12 mm field size to <0.2% for 60 mm × 60 mm field size) (Figure 8—histograms of dose difference and dose spill for hetero bone). Except for AAA, all other TPS predictions are within 2% of the measured dose. AAA differs from the measured data by approximately 3% for the smallest field (12 mm × 12 mm) considered in this study. The order of agreement with the measured data for central axis dose is MC, followed by Pinnacle, Acuros, PB and AAA TPS.
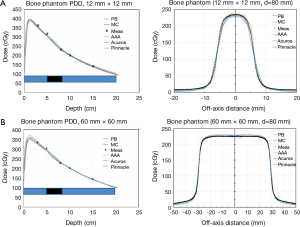
Based on the PDD behavior, Acuros XB and Pinnacle represent the closest agreement with MC within bone including the interface region from bone to tissue. AAA shows a slight over-prediction of dose.
The behavior of dose spill in the bone phantom shows the dependence on field size with larger fields showing greater difference with measured doses. Among various TPS, Pinnacle shows the largest difference with MC and measured doses in the penumbra region.
Phantom 4: dual lung target phantom
Figure 9 shows PDD and dose profile comparisons for the dual lung target phantom for 30 mm × 30 mm and 60 mm × 60 mm fields. Based on PDD comparisons, Pinnacle and MC agree best with measurements throughout. AAA under-predicts dose in the lung region whereas a slight increased dose is seen in Acuros calculations. PB again over predicts dose showing the largest dose discrepancy with measurements in the lung tissue.
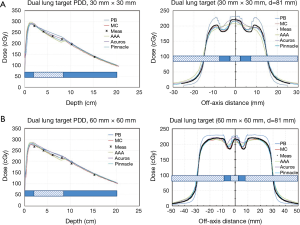
Based on dose profile comparisons, the measured dose is well reproduced within each target by both PB and MC. However, PB algorithm fails in the low-density surrounding medium. Overall, Pinnacle TPS agrees best with the measured data and MC calculations over the entire field size. Acuros XB is accurate in the lung region outside the target but over predicts dose within the target region. Inside the treatment field, AAA algorithm under predicts dose in the low-density regions but over predicts dose in the target. The net result is a smoothed-out AAA dose profile that appears to be insensitive to density difference between target and surrounding lung medium. Outside the treatment field, AAA over predicts dose. These effects are enhanced for smaller fields (30 mm × 30 mm vs. 60 mm × 60 mm).
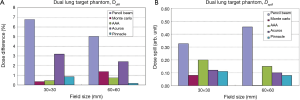
The magnitude of dose disagreement between various dose calculation algorithms and measurements depends on the location in the low-density medium. PB over-predicts measured dose by 4–5% in the lung medium for a 60×60 field size. MC and Pinnacle calculations agree well with measurements throughout the treatment field (<1.5%). In the lung medium between targets for a 30×30 field size, PB over-predicts measured dose by 4.5%. However, in the lung medium surrounding both targets, PB over-predicts delivered dose by up to 12.8%. MC and Pinnacle calculations again agree well with measurements throughout the treatment field (<0.5%) (Figure 10).
In the penumbra region, the PB calculations under-predict delivered dose for both field sizes whereas AAA over-predicts dose outside the treatment field. All other algorithms show good agreement in the penumbra region. These results are consistent with those obtained for the heterogeneous lung phantom. This is reflected in Figure 10 showing results for dose spill comparisons between various dose algorithms and measurements. In the penumbra region, the best agreement is seen with MC followed by Pinnacle, Acuros, AAA and PB TPS.
Discussion
Several previous studies have shown the importance of using MC calculations in lung patient plans (16,18-22). These studies cover a range of treatment sites, photon beam energies and treatment geometries. Some of these studies validate MC calculations in homogeneous phantom and later apply them to heterogeneous phantoms. However, most of these studies are either calculation based showing comparison between MC and other dose models or performed at a single institution often with one or two TPS.
In this study, the importance of MC dose algorithm in lung density medium has been investigated and the results compared in a multi-institutional setting with four other dose algorithms (PBC, AAA, Acuros and Pinnacle) and measured data. These models do reasonably well in calculating doses away from heterogeneities. However, within the heterogeneous medium, some of these models fail to account for lateral electron scatter and thus over predict dose. We have compared MC predictions against various TPS calculations in a variety of phantoms and quantified dose discrepancy versus measured data.
In general, differences between measured dose and TPS calculations get larger with decreasing density of heterogeneous medium, decreasing field size and increasing depth within the heterogeneity. These differences can be as large as 30–40% for PB for small field size (12 mm × 12 mm) based on dose within the central 80% of field size. In regions outside the treatment fields (penumbra region), PB again fails to replicate measured data. Significant under-prediction of dose (up to 50%) by PB model is seen in the penumbra region. MC calculations on the other hand, show excellent agreement with measured dose for all field sizes at all depths for the phantoms considered in this work. Within lung tissue Acuros and Pinnacle provide closest agreement with MC with AAA and PB showing the greatest discrepancy.
The dual lung target phantom provides the most stringent test of MC accuracy and highlights essential differences between various dose models. Based on the results in Figure 9, we see that PB dose between two targets is the same regardless of the field size. However, in regions outside both targets, the 30 mm × 30 mm field shows larger differences between PB and MC when compared with the 60 mm × 60 mm field size. This effect is due to the fact that smaller regions of low density are treated with 30 mm field compared to 60 mm field. However, since the region between both targets is the same in both cases, no difference in PB results is seen. Pinnacle TPS shows the best agreement with MC in both magnitude and shape of dose profiles as well as the behavior near the interface regions. Acuros well reproduces dose in the low-density region surrounding the target but over-predicts dose within the low-density region between dual targets. AAA shows a lack of sensitivity to tissue density variations.
Finite size of calculation grid size can contribute to MC results in interesting ways. For small fields, MC results show somewhat inferior agreement with measurement due to lack of sufficient calculation accuracy (not-shown). We also investigated the role played by the number of particle histories in MC calculations on the quality of fits by reducing statistical variance to 0.1%. However, this did not have a significant effect on our results.
An interesting behavior is noted with respect to PB calculations. When compared to measured data, the magnitude of PB over-prediction is inversely proportional to field size at a given depth in phantom (Figure 5). Knowing the dose over prediction for a given field size, one can estimate it for any other field size by a simple scale factor. This may be important when determining ideal treatment margins for small targets in lung SBRT planned with PB type algorithms.
In our work, we have also studied the importance of using two new dose profile indices. The dose difference index (Ddiff) is a measure of dose enhancement in the central 80% of field size. This is directly proportional to the dose received by the target. The dose spill index (Dspill) evaluates dose in regions outside the target. This may be important in evaluating dose in the periphery of the target as well as dose received by nearby critical structures.
A limitation of the present study is that only 6MV photons were investigated. The effect of heterogeneity corrections may be more exaggerated at higher energies. However, since most of the treatment plans for lung SBRT are performed with volumetric modulated arc therapy (VMAT) at lower (6MV) energies, the presented results will be useful for clinics treating patients with SBRT.
Conclusions
A variety of dose calculation algorithms have been used in treatment planning for lung SBRT patients. These range from simple PB convolution method with limited accuracy to 3D CS and the most sophisticated MC model. Predictions from each dose algorithm were compared with measured data for a range of field sizes in custom phantoms composed of tissue, bone and lung equivalent materials. Knowledge of the limitations of each TPS will help optimize treatment planning for lung SBRT patients in the clinic. The results of this multi-institutional study may further help clarify dose differences seen in patients enrolled on protocol studies.
Acknowledgments
Funding: None.
Footnote
Conflicts of Interest: AS serves as an unpaid editorial board member of Therapeutic Radiology and Oncology from Sep 2018 to Sep 2020. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- AAPM. The American Association of Physicists in Medicine (AAPM) Report 85 Tissue inhomogeneity corrections for MV photon beams. USA: Report of Task Group No. 65 of AAPM, 2004.
- ICRU 1976 Determination of absorbed dose in a patient irradiated by beams of x or gamma rays in radiotherapy procedures Report 24 (Washington, DC: International Commission on Radiation Units and Measurements).
- Chen H, Lohr F, Fritz P, et al. Stereotactic, single-dose irradiation of lung tumors: a comparison of absolute dose and dose distribution between pencil beam and Monte Carlo algorithms based on actual patient CT scans. Int J Radiat Oncol Biol Phys 2010;78:955-63. [Crossref] [PubMed]
- Fragoso M, Wen N, Kumar S, et al. Dosimetric verification and clinical evaluation of a new commercially available Monte Carlo-based dose algorithm for application in stereotactic body radiation therapy (SBRT) treatment planning. Phys Med Biol 2010;55:4445-64. [Crossref] [PubMed]
- Carrasco P, Jornet N, Duch MA, et al. Comparison of dose calculation algorithms in phantoms with lung equivalent heterogeneities under conditions of lateral electronic disequilibrium. Med Phys 2004;31:2899-911. [Crossref] [PubMed]
- Pai S, Das I, Dempsey J, et al. TG-69: Radiographic film for megavoltage beam dosimetry. Med Phys 2007;34:2228-58. [Crossref] [PubMed]
- Mohan R, Chui C, Lidofsky L. Differential pencil beam dose computation model for photons. Med Phys 1986;13:64-73. [Crossref] [PubMed]
- Ahnesjö A, Saxner M, Trepp A. A pencil beam model for photon dose calculation. Med Phys 1992;19:263-73. [Crossref] [PubMed]
- Fippel M. Fast Monte Carlo dose calculation for photon beams based on the VMC electron algorithm. Med Phys 1999;26:1466-75. [Crossref] [PubMed]
- Kawrakow I, Fippel M. Investigation of variance reduction techniques for Monte Carlo photon dose calculation using XVMC. Phys Med Biol 2000;45:2163-83. [Crossref] [PubMed]
- Ahnesjö A. Collapsed cone convolution of radiant energy for photon dose calculation in heterogeneous media. Med Phys 1989;16:577-92. [Crossref] [PubMed]
- Mackie TR, Reckwerdt PJ, McNutt TR, et al. "Photon beam dose computations" Teletherapy: Proceedings of the 1996 AAPM Summer School. In: Palta J, Mackie TR. editors. AAPM-College Park, MD, 1996:103-35.
- Ulmer W, Kaissl W. The inverse problem of a Gaussian convolution and its application to the finite size of the measurement chambers/detectors in photon and proton dosimetry. Phys Med Biol 2003;48:707-27. [Crossref] [PubMed]
- Ulmer W, Pyyry J, Kaissl W. A 3D photon superposition/convolution algorithm and its foundation on results of Monte Carlo calculations Phys. Med. Biol 2005;50:1767-90. [Crossref] [PubMed]
- Fogliata A, Nicolini G, Clivio A, et al. Critical appraisal of Acuros XB and Anisotropic Analytic Algorithm dose calculation in advanced non-small-cell lung cancer treatments. Int J Radiat Oncol Biol Phys 2012;83:1587-95. [Crossref] [PubMed]
- Han T, Mikell JK, Salehpour M, et al. Dosimetric comparison of Acuros XB deterministic radiation transport method with Monte Carlo and model-based convolution methods in heterogeneous media. Med Phys 2011;38:2651-64. [Crossref] [PubMed]
- Kroon PS, Hol S, Essers M. Dosimetric accuracy and clinical quality of Acuros XB and AAA dose calculation algorithm for stereotactic and conventional lung volumetric modulated arc therapy plans. Radiat Oncol 2013;8:149. [Crossref] [PubMed]
- Fogliata A, Vanetti E, Albers D, et al. On the dosimetric behavior of photon dose calculation algorithms in the presence of simple geometric heterogeneities: comparison with Monte Carlo calculations. Phys Med Biol 2007;52:1363-85. [Crossref] [PubMed]
- Jang SY, Liu HH, Wang X, et al. Dosimetric verification for intensity-modulated radiotherapy of thoracic cancers using experimental and Monte Carlo approaches. Int J Radiat Oncol Biol Phys 2006;66:939-48. [Crossref] [PubMed]
- Haedinger U, Kreiger T, Flentje M, et al. Influence of calculation model on dose distribution in stereotactic radiotherapy for pulmonary targets. Int J Radiat Oncol Biol Phys 2005;61:239-49. [Crossref] [PubMed]
- Wu JK, Lee C, Agazaryan N, et al. Monte Carlo vs. pencil beam algorithm with and without tissue heterogeneity correction in stereotactic body radiation therapy for lung tumors. Int J Radiat Oncol Biol Phys 2009;75:S441. [Crossref]
- Wilcox EE, Daskalov GM, Lincoln H, et al. Comparison of planned dose distributions calculated by Monte Carlo and ray-trace algorithms for the treatment of lung tumors with cyberknife: a preliminary study in 33 patients. Int J Radiat Oncol Biol Phys 2010;77:277-84. [Crossref] [PubMed]
Cite this article as: Chopra KL, Leo P, Kabat C, Rai DV, Avadhani JS, Kehwar TS, Sethi A. Evaluation of dose calculation accuracy of treatment planning systems in the presence of tissue heterogeneities. Ther Radiol Oncol 2018;2:28.